E資格受験に必要なJDLA認定講座の一つであるラビット・チャレンジ(https://ai999.careers/rabbit/)のレポート用ページです。
100文字以上要点まとめ
活性化関数を使うことでニューラルネットワークの表現力がぐっと上がる
活性化関数の効果で一部の出力は弱く、一部は強く伝播される。
中間層用の活性化関数
・ステップ関数
現在はほとんど使われない
課題:0-1の間を表現できず、線形分離可能なものしか学習できない
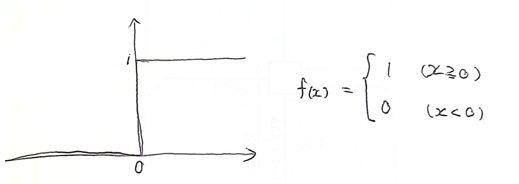
・シグモイド関数
微分可能なので学習に使いやすい
課題:大きな値では出力の変化が微小なため勾配消失問題を引き起こすことがあった

・RELU関数
シグモイド関数の勾配消失問題を回避するために作られた
今もっとも使われている活性化関数
勾配消失問題の解消、スパース化の効果

出力層用の活性化関数
⇒(Section3を参照)
実装演習
確認テスト
①線形非線形の違いを図に書いて簡易に説明せよ
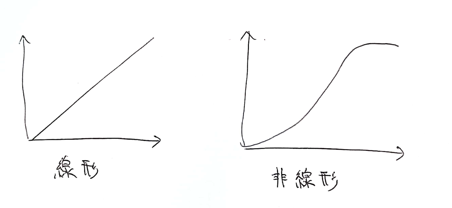
線形な関数は
・加法性:f(x+y) = f(x) + f(y)
・斎次性:f(kx) = kf(x)
を満たす
非線形な関数は加法性・斎次性を満たさない
②配布されたソースコードより該当する箇所を抜き出せ


時間
12/11 00:45

コメント