【ラビットチャレンジレポート】深層学習day1　Section5：誤差逆伝播

E資格受験に必要なJDLA認定講座の一つであるラビット・チャレンジ(https://ai999.careers/rabbit/)のレポート用ページです。

100文字以上要点まとめ

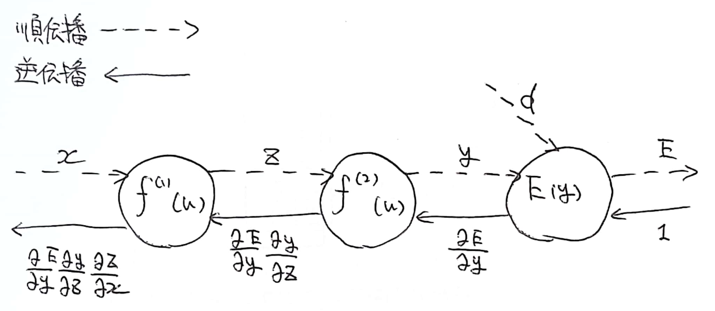
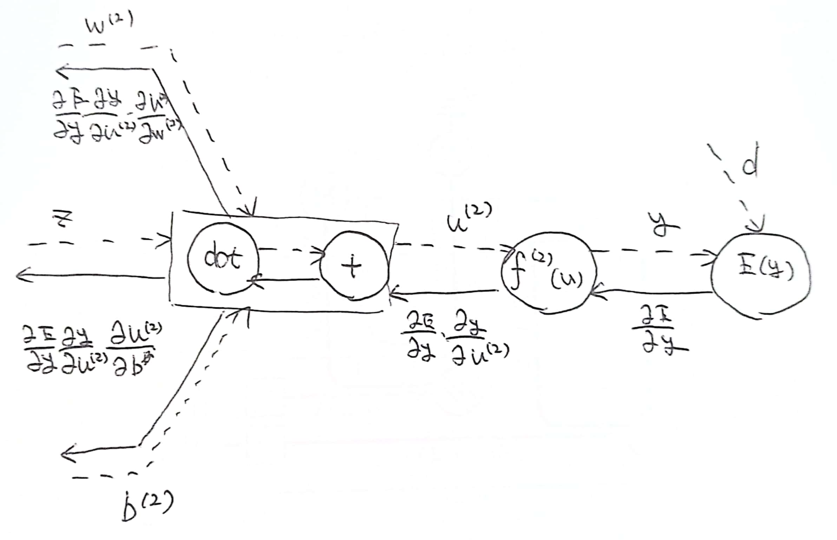
算出された誤差を出力層から順に微分し前の層前の層へと伝播
各パラメータの微分値を解析的に計算する方法

\( E(y) \frac{1}{2}{||y-d||^2} \)
\( \frac{\partial E(y)}{\partial y} = y-d \)
\( \frac{\partial y(u)}{\partial u} = \frac{\partial u}{\partial u} = 1 (恒等写像の場合) \)
\( \frac{\partial u(w)}{\partial w_{ji}} = \frac{\partial}{\partial w_{ji}} ( wz+b ) = [ 0 … z_i … 0]^T\)

実装演習

エビデンス

確認テスト

①誤差逆伝播法では不要な再帰的処理を避ける事が出来る。既に行った計算結果を保持しているソースコードを抽出せよ。

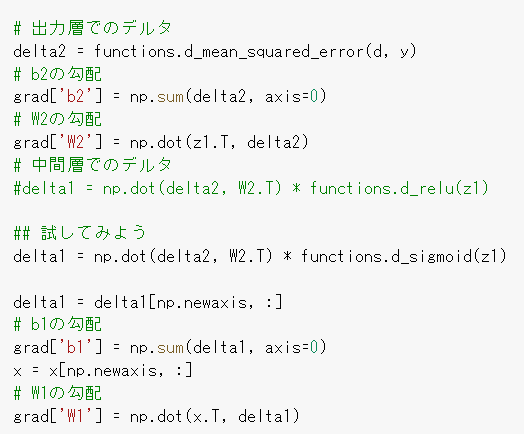
②下記2式に該当するソースコードを探せ

\(\frac{\partial E(y)}{\partial y}\frac{\partial y(u)}{\partial u} \)

\( \frac{\partial E(y)}{\partial y} \frac{\partial y(u)}{\partial u} \frac{\partial u(w)}{\partial w_{ji}^{(2)}} \)

時間

12/11 1:20